Symmetrie zum Ursprung
Die Symmetrie zum Ursprung wird auch ungerade Symmetrie genannt, weil bei einer ungeraden Symmetrie alle Hochzahlen von x ungerade sind. Befindet sich eine Zahl ohne x in der Funktion ist diese auch als gerade zu werten, selbst wenn die Zahl ungerade ist. An den ungeraden Hochzahlen erkennt man die gerade Symmetrie (Symmetrie zur y-Achse).
Zudem kann die ungerade Symmetrie mit folgender Formel geprüft werden:
f(-x) = -f(x)
Symmetrie zum Ursprung Beispiel:
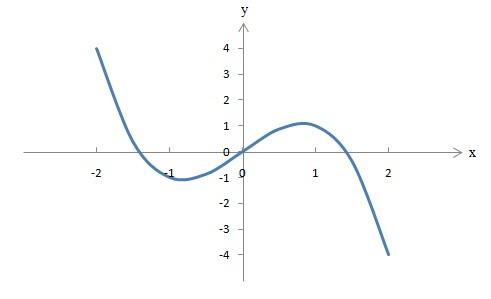
f(x) = -x³+2x
Anhand der ungeraden Hochzahlen(Exponenten) fällt bereits auf, dass es sich hierbei um eine ungerade Symmetrie handelt. Dies lässt sich auch mit folgender Formel nachprüfen:
f(-x) = -f(x)
-(-x)³+2(-x) = – (-x³+2x) Einsetzen eines beliebigen x-Werts x = 1
-(-1)³ + 2 × -1 =-(-(1)³ + 2 × 1)
1+(-2) = -(-1 +2)
1 – 2 = -(-1 + 2)
1 = -(1)
1 = 1
Da das gleiche Ergebnis herauskommt ist es eine ungerade Symmetrie. Dies zeigt auch das Schaubild der Funktion f(x) = -x³+2x, da die Funktiom am Ursprung gespiegelt wird.