Die Nullstellen eines Graphen lassen sich nicht auf eine universell gültige Weise bestimmen – es sind häufig andere Hilfsformeln nötig die immer mehr oder weniger schwierig sind.
Was jedoch immer gilt ist dass die Funktion gesetzt werden muss. Danach muss man auch immer die Funktionsgleichung nach auflösen – allerdings geschieht dies oft auf eine andere Art und Weise. Die evtl. anwendbaren Verfahren sind hier nach der Einfachheit sortiert – angefangen beim einfachsten, aufgehört beim kompliziertesten.
Allgemein gilt übrigens, dass eine Funktion maximal so viele Nullstellen haben kann wie hoch ihr Grad ist!
1.) Umformen der Formel
Es kann Funktionsgleichungen geben, bei denen man durch einfaches Umformen auf die Lösung kommen kann. Eine Funktion bei der dies anwendbar wäre ist zum Beispiel f(x)=x^2-4 . Hierbei
lässt sich diese Funktion auf einfache Weise nach x auflösen:
Achtung: Beim Ziehen der Wurzel wie in diesem Fall ist immer zu beachten, dass das sowohl positiv als auch negativ sein könnte um die Gleichung zu erfüllen!
2.) Ausklammern
Bei allen Funktionen die keine Konstante (d.h. keinen Wert ohne X haben) lässt sich etwas ausklammern. Die auszuklammernde Variable ist dabei meistens X . Ein Funktionsbeispiel hierfür wäre die Funktion f(x)=x^2-4 .
Nun haben wir zwei Faktoren. Einmal x und einmal (x-4) und es ist logischerweise egal welcher von beiden ist. Von daher können wir die Linearfaktoren als getrennte Funktionen betrachten, deren Nullstellen jeweils den Nullstellen der Ausgangsfunktion entsprechen:
Diese Funktion hat also eine Nullstelle bei 0 und eine bei 4 .
3.) Mitternachtsformel oder ABC Formel
Die ABC- oder Mitternachtsformel lässt sich generell bei Gleichungen der Form 
anwenden, also bei quadratischen Gleichungen. Ein Beispiel hierfür könnte unter anderem die Funktion 
. Allerdings müsste man bei dieser Funktion zunächst
ausklammern. Dieses Beispiel soll auch zeigen, dass häufig Kombinationen aus den verschiedenen Methoden nötig sind:
Als erste Nullstelle haben wir nun selbstverständlich x=0 aus dem Linearfaktor x. Aus dem zweiten Linearfaktor (2x^2+4x+2) können wir nun mithilfe der Mitternachtsformel die weiteren
Nullstellen bestimmen. Die Mitternachtsformel lautet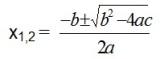 
, wobei a die Zahl vor dem x^2 ist b, die Zahl vor x ist sowie c die Konstante ist. Also:
Die zweite Nullstelle ist also x= -1. Eine dritte Nullstelle existiert bei dieser Funktion nicht, da unter der Wurzel 0 steht.
4.) PQ Formel
Zur PQ Formel haben wir hier einen ausführlichen Artikel: PQ Formel Erklärung
5.) Substitution
Die Substitution ist das komplizierteste Verfahren zur Nullstellenbestimmung. Dabei werden bestimmte Potenzen von x durch eine Variable zunächst ersetzt. Dann wird nach dieser Variable aufgelöst und es wird wieder in die Ausgangsvariable übersetzt. Das ist so ohne Beispiel schwer zu verstehen. Eine Beispielfunktion wäre 
.
Hierbei könnte man x^2=z setzen, dann hätte man für die Funktion nur noch 
was wiederum eine Funktion wäre die man mit der Mitternachtsformel auflösen könnte:
So jetzt kennt ihr viele Möglichkeiten um Nullstellen zu berechnen bzw. zu bestimmen, wählt die aus, die euch am leichtesten fällt.
Schreibe einen Kommentar